Công thức tính đường trung tuyến trong tam giác

Công thức tính độ dài đường trung tuyến Toán 10 để bạn đọc cùng tham khảo. Bài viết được tổng hợp nội dung kiến thức của bài học về định nghĩa đường trung tuyến trong tam giác, tính chất đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều và công thức tính độ dài đường trung tuyến trong tam giác, mời các em học sinh cùng tham khảo chi tiết và tải về bài viết dưới đây nhé. Chúc các bạn học tập tốt!

Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

1. Đường trung tuyến

Đường trung tuyến là gì?

- Đường trung tuyến của 1 đoạn thẳng là 1 đường thẳng đi qua trung điểm của đường thẳng đó.

- Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của các cạnh đối diện nó. Mỗi tam giác có 3 đường trung tuyến.

Ví dụ: Cho tam giác ABC, có D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC. Từ đó ta có các đường thẳng BD, AF, CE là các đường trung tuyến của tam giác ABC.

Cách vẽ đường trung tuyến

Bước 1: Vẽ tam giác ABC.

Bước 2: Vẽ trung điểm của đoạn thẳng BC, đặt tên điểm này là M.

Bước 3: Vẽ trung điểm của đoạn thẳng AB, đặt tên điểm này là P.

Bước 4: Vẽ trung điểm của đoạn thẳng AC, đặt tên điểm này là N.

Bước 5: Vẽ trung tuyến AM.

Bước 6: Vẽ trung tuyến BN.

Bước 7: Vẽ trung tuyến CP.

Bước 8: Vẽ giao điểm của AM; BN và CE, đặt tên giao điểm này là G.

2. Tính chất đường trung tuyến trong tam giác

a. Tính chất đường trung tuyến trong tam giác

- Ba đường trung tuyến của tam giác đồng quy tại một điểm được gọi là trọng tâm.

- Khoảng cách từ trong tâm đến mỗi đỉnh của tam giác bằng (frac{2}{3}) đường trung tuyến tương ứng với đỉnh đó.

- Khoảng cách từ trong tâm đến trung điểm mỗi cạnh bằng đường 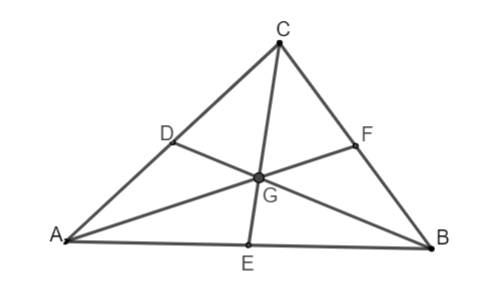(frac{1}{3}) trung tuyến tương ứng với điểm đó.

Ví dụ: Cho tam giác ABC, có D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC.

- Gọi G là giao điểm của các đường thẳng BD, AF, CE suy ra G là trọng tâm tam giác ABC.

Ta có các tính chất sau:

(frac{{CG}}{{CE}} = frac{{AG}}{{AF}} = frac{{BG}}{{BD}} = frac{2}{3})

(frac{{GE}}{{CE}} = frac{{GF}}{{AF}} = frac{{GD}}{{BD}} = frac{1}{3})

b. Tính chất đường trung tuyến trong tam giác vuông

- Đường trung tuyến của tam giác vuông có các tính chất chung của đường trung tuyến trong tam giác thường. Ngoài ra ta có các tính chất đặc trưng sau:

+ Đường trung tuyến trong tam giác vuông ứng với cạnh huyền bằng một nửa cạnh huyền.

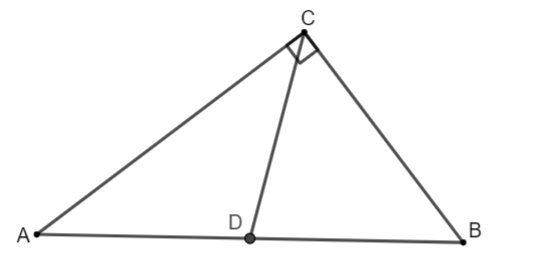
Ví dụ: Cho tam giác ABC vuông tại C, đường trung tuyến CD:

(begin{matrix} Rightarrow CD = dfrac{1}{2}AB hfill Rightarrow CD = AD = DB hfill end{matrix})

+ Trong một tam giác có đường trung tuyến ứng với một cạnh mà bằng một nửa cạnh đó thì tam giác đó là tam giác vuông.

c. Tính chất đường trung tuyến trong tam giác cân, tam giác đều

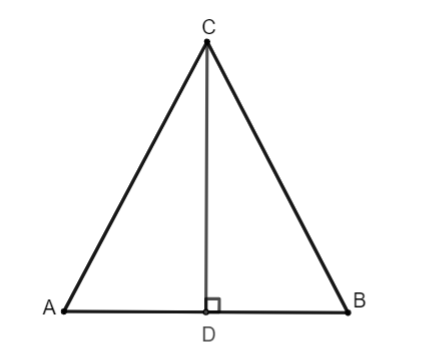
- Trong tam giác cân, tam giác đều, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đó và chia tam giác thành hai tam giác bằng nhau.

Ví dụ:

Ví dụ: Trong hình sau, G là trọng tâm tam giác ABC.

a. Tìm x biết 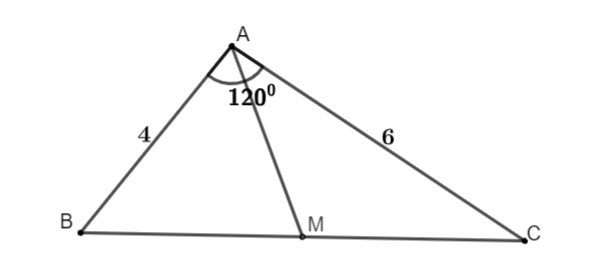(AG = 4x + 6,AM = 9x)?

b. Tìm x biết 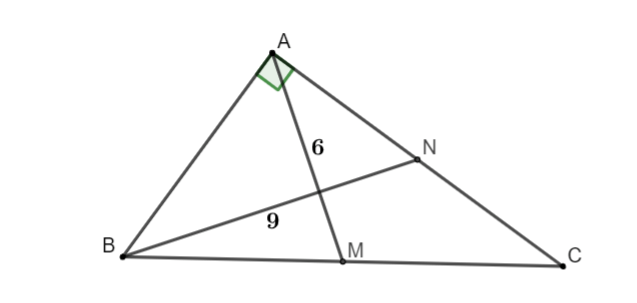(CG = 5x,GN = 3x - 2)?

Hướng dẫn giải

a. Áp dụng tính chất trọng tâm ta có

(AG = frac{2}{3}AM)(Rightarrow 4x + 6 = frac{2}{3}.9x)

(Rightarrow 3(4x + 6) = 18x)(Rightarrow 12x + 18 = 18x)

(Rightarrow 6x = 18 Rightarrow x = 3)

b. Áp dụng tính chất trọng tâm ta có

(CG = 2GN)(Rightarrow 5x = 2(3x - 2))

(Rightarrow 5x = 6x - 4)(Rightarrow x = 4)

Ví dụ: Cho tam giác ABC có AB = AC = 5cm; BC = 8cm, đường trung tuyến (AM), trọng tâm (G). Tính độ dài đoạn thẳng AG?

Hướng dẫn giải

Hình vẽ minh họa

Xét ∆AMB và ∆AMC có

AM là cạnh chung

AB = AC (giả thiết)

MA = MB (M là trung điểm của BC)

=> ∆AMB = ∆AMC

(Rightarrow widehat{AMB} = widehat{AMC}) vì (widehat{AMB} + widehat{AMC} = widehat{BMC} = 180^{0}) nên (widehat{AMB} = widehat{AMC} = 90^{0})

(Rightarrow AMbot BC)

Áp dụng định lý Py-ta-go cho tam giác AMB vuông tại M

(AB^{2} = AM^{2} + BM^{2})

(Rightarrow AM^{2} = AB^{2} - BM^{2} = 5^{2} - 4^{2} = 9)

(Rightarrow AM = 3(cm))

Ví dụ: Cho tam giác ABC cân tại A. Vẽ hai đường trung tuyến AM và BN. Cho biết AM = 9cm, BC = 8cm. Tính độ dài BN?

Hướng dẫn giải

Hình vẽ minh họa

Xét ∆AMB và ∆AMC có

AM là cạnh chung

AB = AC (giả thiết)

MA = MB (M là trung điểm của BC)

=> ∆AMB = ∆AMC

(Rightarrow widehat{AMB} = widehat{AMC}) vì (widehat{AMB} + widehat{AMC} = widehat{BMC} = 180^{0}) nên (widehat{AMB} = widehat{AMC} = 90^{0})

(Rightarrow AMbot BC)

Gọi G là giao điểm của AM và BN. Khi đó G là trọng tâm ∆ABC

(BM = frac{BC}{2} = 4(cm))

(GM = frac{1}{3}AM = 3(cm))(tính chất trọng tâm)

Áp dụng định lí Pythagore cho tam giác GBM vuông tại M.

(BG^{2} = GM^{2} + BM^{2} = 3^{2} + 4^{2} = 25)

=> BG = 5(cm)

Theo tính chất trọng tâm (BG = frac{2}{3}BN Rightarrow BN = frac{3}{2}BG = frac{3}{2}.5 = 7,5)

3. Công thức đường trung tuyến

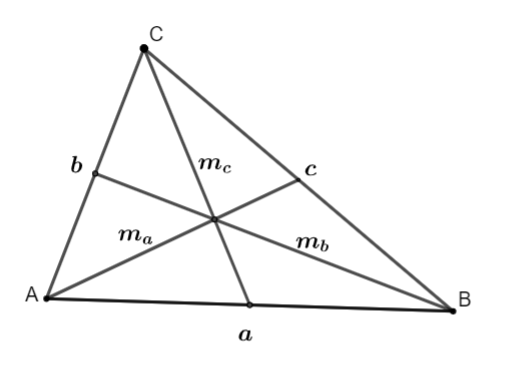
Cho tam giác ABC có độ dài các cạnh AB = c; AC = b; BC = a, các đường trung tuyến ({m_a};{m_b};{m_c})

Hình vẽ minh họa

(begin{matrix} {m_a}^2 = dfrac{{{b^2} + {c^2}}}{2} - dfrac{{{a^2}}}{4} hfill {m_b}^2 = dfrac{{{a^2} + {c^2}}}{2} - dfrac{{{b^2}}}{4} hfill {m_c}^2 = dfrac{{{a^2} + {b^2}}}{2} - dfrac{{{c^2}}}{4} hfill end{matrix})

4. Bài tập ví dụ minh họa

Hướng dẫn giải

a.

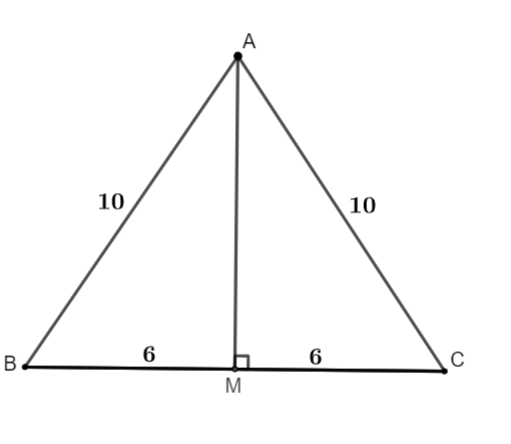
Hình vẽ minh hoạ:

Ta có tam giác ABC cân tại A, AM là trung tuyến suy ra AM là đường cao, đường phân giác của tam giác ABC

(Rightarrow BM = MC = frac{1}{2}BC = 6)

Áp dụng định lý Pi - ta - go cho tam giác vuông AMC có:

(A{C^2} = A{M^2} + M{C^2} Rightarrow AM = sqrt {A{C^2} - M{C^2}} = 8)

b.

Hình vẽ minh họa

Ta có: (B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos {120^0})

(Rightarrow BC = 2sqrt {19})(Rightarrow A{M^2} = frac{{A{B^2} + A{C^2}}}{2} - frac{{B{C^2}}}{4})

(Rightarrow AM = sqrt 7)

Hướng dẫn giải

Hình vẽ minh họa:

Tam giác ABC vuông tại A, AM là trung tuyến nên AM = BM = MC = 6

Suy ra BC = 12

Mặt khác:

(begin{matrix} left{ {begin{array}{*{20}{c}} {A{M^2} = dfrac{{A{B^2} + A{C^2}}}{2} - dfrac{{B{C^2}}}{4}} {B{N^2} = dfrac{{B{C^2} + A{B^2}}}{2} - dfrac{{A{C^2}}}{4}} end{array}} right. Rightarrow left{ {begin{array}{*{20}{c}} {dfrac{{A{B^2} + A{C^2}}}{2} = 72} {dfrac{{A{B^2}}}{2} - dfrac{{A{C^2}}}{4} = 45} end{array}} right. hfill Rightarrow left{ {begin{array}{*{20}{c}} {A{B^2} = 54} {A{C^2} = 18} end{array}} right. Rightarrow left{ {begin{array}{*{20}{c}} {AB = 3sqrt 6 } {AC = 3sqrt 2 } end{array}} right. hfill hfill end{matrix})

Hướng dẫn giải

a) Ta có:

Độ dài đường trung tuyến AM của tam giác đã cho có độ dài là:

(MA = sqrt {frac{{A{B^2} + A{C^2}}}{2} - frac{{B{C^2}}}{4}})(= sqrt {frac{{{2^2} + {6^2}}}{2} - frac{{{5^2}}}{4}} = frac{{sqrt {55} }}{2}).

Chọn đáp án A.

b) Hình vẽ minh họa:

Ta có: (cos A = frac{{{b^2} + {c^2} - {a^2}}}{{2bc}})(= frac{{{{14}^2} + {{15}^2} - {{13}^2}}}{{2.14.15}} = frac{3}{5})

Gọi M là trung điểm của AC.

Trong tam giác ABM, ta có:

(B{M^2} = A{B^2} + A{M^2} - 2AB.AM.cos A)

(= {15^2} + {7^2} - 2.15.7.frac{3}{5} = 148)(Rightarrow BM = 2sqrt {37}).

Chọn đáp án B.

c. Ta có:

(m_a^2 = frac{{{b^2} + {c^2}}}{2} - frac{{{a^2}}}{4})(= frac{{{6^2} + {5^2}}}{2} - frac{{{3^2}}}{4} Rightarrow {m_a} = frac{{sqrt {113} }}{2}).

Chọn đáp án A.

d) Độ dài đường trung tuyến AM của tam giác ABC là:

(MA = sqrt {frac{{A{B^2} + A{C^2}}}{2} - frac{{B{C^2}}}{4}})(= sqrt {frac{{{9^2} + {{12}^2}}}{2} - frac{{{{15}^2}}}{4}} = 7,5) (cm)

Chọn đáp án C.

Hướng dẫn giải:

Gọi G là trọng tâm tam giác ABC. Ta có:

(A{M^2} = frac{{A{C^2} + A{B^2}}}{2} - frac{{B{C^2}}}{4} = frac{{{b^2} + {c^2}}}{2} - frac{{{a^2}}}{4}) (Công thức tính đường trung tuyến trong tam giác)

(Rightarrow A{G^2} = frac{4}{9}A{M^2} = frac{{2left( {{b^2} + {c^2}} right)}}{9} - frac{{{a^2}}}{9})

(B{N^2} = frac{{B{A^2} + B{C^2}}}{2} - frac{{A{C^2}}}{4} = frac{{{c^2} + {a^2}}}{2} - frac{{{b^2}}}{4})

(Rightarrow G{N^2} = frac{1}{9}B{N^2} = frac{{{c^2} + {a^2}}}{{18}} - frac{{{b^2}}}{{36}})

Trong tam giác AGN ta có:

(cos widehat {AGN} = frac{{A{G^2} + G{N^2} - A{N^2}}}{{2.AG.GN}})

(= dfrac{{dfrac{{2left( {{b^2} + {c^2}} right)}}{9} - dfrac{{{a^2}}}{9} + dfrac{{{c^2} + {a^2}}}{{18}} - dfrac{{{b^2}}}{{36}} - dfrac{{{b^2}}}{4}}}{{2.sqrt {dfrac{{2left( {{b^2} + {c^2}} right)}}{9}} - dfrac{{{a^2}}}{9}.sqrt {dfrac{{{c^2} + {a^2}}}{{18}} - dfrac{{{b^2}}}{{36}}} }})

(= dfrac{{dfrac{{2left( {{b^2} + {c^2}} right)}}{9} - dfrac{{{a^2}}}{9} + dfrac{{{c^2} + {a^2}}}{{18}} - dfrac{{{b^2}}}{{36}} - dfrac{{{b^2}}}{4}}}{{2.sqrt {dfrac{{2left( {{b^2} + {c^2}} right)}}{9} - dfrac{{{a^2}}}{9}} .sqrt {dfrac{{{c^2} + {a^2}}}{{18}} - dfrac{{{b^2}}}{{36}}} }})

(= dfrac{{10{c^2} - 2left( {{a^2} + {b^2}} right)}}{{36.2.sqrt {dfrac{{2left( {{b^2} + {c^2}} right)}}{9} - dfrac{{{a^2}}}{9}} .sqrt {dfrac{{{c^2} + {a^2}}}{{18}} - dfrac{{{b^2}}}{{36}}} }} = 0)

(Rightarrow widehat {AGN} = {90^0}).

-

Trên đây VnDoc đã giới thiệu tới các bạn bài Công thức đường trung tuyến Toán 10. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết tổng hợp những công thức đường trung tuyến, khái niệm đường trung tuyến, tính chất đường trung tuyến trong tam giác, kèm theo đó là những ví dụ, bài tập luyện tập có lời giải chi tiết kèm theo. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!